В.Б.Губин. О физике, математике и методологии. - М.: ПАИМС. 2003.

Труды семинара “Время, хаос и математические проблемы”.
Вып. II. - М.: Книжный дом “Университет”. 2001 г. С. 177-192.

В.Б.Губин

I. ВВЕДЕНИЕ.

Проблеме согласования термодинамики и механики больше ста лет. Многие привыкли к традиционным “учебниковым” интерпретациям и к их же недосказанностям. Предлагаемый здесь подход мог бы появиться уже во времена Максвелла или в крайнем случае Смолуховского. Поэтому, во-первых, физикам следует перенестись мысленно в начало века и на время отвлечься от традиционных квазиобъяснений, содержащих слова “распределение” и “ансамбль”, которые сами требуют сложного разъяснения. Во-вторых, не следует всуе поминать слово “природа”, так как рассматриваемая проблема касается согласования четко определенных, фактически математических моделей, существующих на бумаге. Математики же должны с пониманием отнестись к тому, что физические доказательства не являются чисто формально-логическими. Это в математике не возникает сомнений, когда в доказательстве можно и следует поставить точку. В физике же главным критерием правильности подхода является его естественная согласованность со всем другим знанием, чего без некоторой интуиции невозможно увидеть.

II. ТРУДНОСТИ СОГЛАСОВАНИЯ ТЕРМОДИНАМИЧЕСКОЙ НЕОБРАТИМОСТИ
С МЕХАНИЧЕСКОЙ ОБРАТИМОСТЬЮ.

2-й закон термодинамики не связывает монотонную направленность движения в одну сторону - к равновесию (к максимуму энтропии) - с начальными условиями. С другой стороны, набор частиц, входящих в состав термодинамической системы и движущихся по механике, имеет полное право двигаться как в одну сторону, так и в противоположную - в зависимости от знаков скоростей, т.е. от начальных условий, причем, по-видимому, эти противоположные варианты должны реализовываться практически равновероятно.

Противоречие этого вида было обнаружено больше 120 лет назад. В 1872 г. Больцман на основе своего кинетического уравнения доказал знаменитую Н-теорему. Он рассматривал изменение распределения частиц газа по скоростям в результате взаимных столкновений частиц. У него получилось монотонное изменение распределения в сторону увеличения энтропии с предельным состоянием в виде максвелловского распределения. (В связи с этим вспоминается известная физическая теорема: через две точки всегда можно провести кривую, притом единственным образом.) На это доказательство возразил Лошмидт, указав, что если в какой-то момент движения к равновесию обратить скорости, то в соответствии с механикой система пойдет обратно, удаляясь от равновесия, и это будет стопроцентно для всех систем, а термодинамика это запрещает. В ответ Больцман якобы сказал: “Пойдите и обратите их!” С одной стороны, верно, но с другой - все же остается неясным, с какой стати одно направление скоростей оказывается стопроцентно предпочтительным.

Позже на основании теоремы Лиувилля о сохранении фазового объема механической системы Пуанкаре доказал возвратную теорему: для замкнутой изолированной системы можно указать конечное время, в течение которого фазовая точка системы хотя бы один раз вернется в заданную окрестность исходной точки. Цермело обратил утверждение этой теоремы против доказательств одностороннего движения систем из механических частиц. И это было правильно.

Кстати говоря, объяснение Пригожиным необратимости с помощью его “принципа отбора” - предположения о выборе природой только тех наборов скоростей, которые приводят к движению в сторону роста энтропии, - должно быть отвергнуто, в частности, также из-за возвратной теоремы, так как никакой выбор начальных скоростей не уничтожает квазиобратимости.

III. ОБЪЯСНЕНИЕ НЕОБРАТИМОСТИ СМОЛУХОВСКИМ.

В начале XX века Смолуховский показал, что возникает лишь впечатление необратимости: “...кажущиеся необратимыми процессы в действительности являются обратимыми.” [1] “Представляется ли нам какой-либо ... процесс обратимым или необратимым..., зависит ... только от начального состояния и от продолжительности наблюдения.” [2]

Движущиеся частицы редко группируются так, чтобы образовывалось сильно неравновесное состояние. Наблюдатель же практически видит только большие отклонения, которые после рассасывания возникают вновь очень редко, через огромные (в среднем) промежутки времени, и из-за ограниченности времени наблюдения их возвраты не наблюдаются. В механике (фактически - в математике) нет понятий “нерезко” (видно), “долго” (ждать) и “много” (частиц), поэтому она сама не может примириться с необратимостью, а для человека они есть, и в широких условиях он видит необратимость.

Объяснение Смолуховского было большинством физиков принято как в высшей степени естественное. Но с течением времени и по мере нарастания формализаторских тенденций в физике термодинамическая необратимость постепенно стала снова рассматриваться вполне объективистски как закон природы, существующий без наблюдателя. Во втором (синем) издании “Большой советской энциклопедии” работы Смолуховского по этим вопросам упоминаются, а в третьем (красном) издании уже нет. А вот заявление Л.Д.Ландау и Е.М.Лифшица в курсе “Статистическая физика” [3]: “...связывание физических законов со свойствами наблюдателя, разумеется, совершенно недопустимо.” А в итоге: “Вопрос о физических основаниях закона монотонного возрастания энтропии остается ... открытым.” Пригожин также отвергал принципиальную роль наблюдателя в трактовке необратимости. [4]

IV. ПРИГОТОВЛЕНИЕ НЕРАВНОВЕСНОГО СОСТОЯНИЯ.
ТЕРМОДИНАМИКА НЕ ВЫДЕЛЯЕТ НАПРАВЛЕНИЯ ВРЕМЕНИ.

Смолуховский разъяснил общую тенденцию систем стремиться к равновесию в конечном счете, причем в обоих направлениях времени, без выделения его знака. Это является необходимым условием согласования термодинамики с механикой. Он не разъяснил более локального случая.

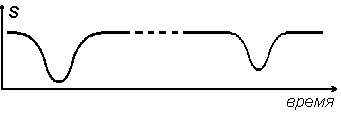
Когда мы попадаем в отклонение от равновесия, то почему никогда не оказываемся на левом его склоне? (Чтобы не попадать на левый склон, раньше даже представляли вместо

Рис. 1.

кривой из рис.1 патологическую кривую, имеющую минимум в каждой точке, но не постоянную.) Почему горячий чай никогда сначала не нагревается хотя бы еще немного, чтобы уже потом двинуться без оглядки к равновесию? Ведь разница температур чая и воздуха указывает только на разницу кинетических энергий частиц чая и воздуха, а кинетическая энергия квадратична по скоростям. Знаков скоростей мы не знаем, и все же надежно предсказываем движение в сторону остывания чая!

Ответ получается применением того же подхода Смолуховского.

Пусть у нас есть газ в замкнутом объеме. Мы никогда случайно не попадем в отклонение от равновесия. Поэтому неравновесное состояние надо специально приготавливать. Мы не попадаем в отклонение, а его приготавливаем. А как это сделать? Реально это можно сделать, например, объединением двух взаимно неравновесных систем. Что тогда получится? Берем системы. Подавляюще вероятно, что эти системы по отдельности равновесны. Следовательно, распределения скоростей у них симметричны по знаку. Тогда и в объединенной системе распределение по скоростям также симметрично по знаку. То есть у скольких частиц скорости направлены в одну сторону, у стольких же скорости направлены в противоположную сторону. Какое макроскопическое движение мы тогда увидим?

Пусть у некоторых частиц скорости направлены так, что образуется (макро)движение в сторону равновесия вправо вверх под углом a к горизонтали на кривой зависимости энтропии (или степени равновесия) от времени (как на рис. 1). Но ввиду равновероятности направлений скоростей такой же набор частиц будет образовывать движение в сторону от равновесия, причем с углом (-a ) к горизонтали. Поэтому общее движение в первый момент будет направлено по горизонтали. Это означает, что система была приготовлена в самой глубокой точке отклонения от равновесия. Из этой точки движение может происходить только вверх - как при движении вправо, так и влево, как вперед по времени, так и назад (рис. 2). Чай не нагреется еще больше за счет энергии воздуха - даже если обратить скорости! То есть наблюдаемое движение к равновесию не дает возможности выделить знак времени, термодинамика не выделяет знака времени. Согласование с механикой получено.

Рис. 2

V. ЧТО ТАКОЕ МАКСВЕЛЛОВСКОЕ РАСПРЕДЕЛЕНИЕ ?

Равномерное распределение в координатном пространстве представляется вполне естественным и понятным. Но максвелловское распределение тоже имеет довольно простой смысл. В импульсном пространстве при фиксированной суммарной энергии равномерное заполнение энергетической поверхности дает следующее. Вероятность обнаружить частицу с импульсом в интервале от p до p+dp пропорциональна площади этой поверхности (кольца) между этими плоскостями. Её плотность легко посчитать при одинаковых массах частиц и сферической энергетической поверхности

Оказывается, что эта функция  - длина окружности - сечения сферы плоскостью pi=p - есть

При неограниченном росте числа частиц w стремится к экспоненте:

То есть максвелловское распределение есть иносказание равномерного распределения на энергетической поверхности в пространстве переменных всех импульсов - при большом числе частиц.

при N ® Ґ также переходит в экспоненту.

VI. ВИДИМАЯ ПРИЧИНА НЕОБХОДИМОСТИ ХОЛОДИЛЬНИКА.

Теперь перейдем ко 2-му закону термодинамики в формулировке Томсона: циклической тепловой машине нужен холодильник. При анализе работы тепловой машины выясняется, что надо учесть одну позицию, кажется, совсем чуждую физике, как мы ее понимали. ¹⁾
_________________________________________
¹⁾ Впрочем, А.Пуанкаре говорил в 1904 г.: “…принцип Карно (2-й закон. - В.Г.) есть принцип несовершенный - нечто вроде уступки слабости наших чувств: только потому, что глаза наши недостаточно остры, мы не различаем элементов в смесях; лишь оттого, что наши руки слишком грубы (курсив мой. - В.Г.), мы не можем эти элементы разделить; демон, придуманный Максвеллом, который мог бы сортировать отдельные молекулы, сумел бы дать Вселенной обратный ход”. Неостановимое броуновское движение “противоречит принципу Карно. Если так, то нам более не нужен бесконечно изощренный глаз максвеллова демона, чтобы видеть обратный ход мирового механизма: достаточно нашего микроскопа.” [5]
_________________________________________

Пусть в объеме (цилиндре машины) есть газ. Нагреватель передает ему тепло, и в объеме создается давление. При отодвигании стенки (поршня) давление совершает работу, а газ охлаждается, давление уменьшается.

В циклической машине поршень следует вернуть в исходное положение. Но при вдвигании поршня надо будет затрачивать работу на преодоление давления, причем практически ту же, которая была получена при расширении. То есть за цикл полезной работы не получим. Поэтому перед обратным ходом надо сбросить давление, чтобы затратилась меньшая работа. Сбросить можно путем передачи части тепла другим телам - холодильнику.

Заметим, что здесь холодильник применен для обхода обратимости процесса расширение-сжатие, возникающей при обратимой механике.

VII. ОБ УСЛОВИЯХ ВОЗНИКНОВЕНИЯ КЛАССИЧЕСКОЙ ТЕРМОСТАТИКИ.

И все-таки 2-й закон не есть следствие обратимости механики. Он вообще из одной механики не возникает. Требуется кое-что еще. Это чувствуется уже потому, что механика может сделать все, что не противоречит законам сохранения. Поэтому странно было бы, если бы именно механическая природа (модельного) мира не позволяла использовать всю имеющуюся энергию.

Рассмотрим простейшую модель тепловой машины. Возьмем отрезок (одномерный объем), вдоль которого движется частица, упруго отражаясь от его твердых концов (стенок). Будем медленно отодвигать конец отрезка (поршень). Когда частица ударяется об отодвигающуюся (надвигающуюся) (массивную) стенку, ее скорость после упругого удара уменьшается (увеличивается) на две скорости стенки. Так при отодвигании поршня ему передается часть энергии частицы. В пределе медленных движений стенок по сравнению со скоростью частицы число ударов частицы о стенку стремится к бесконечности, а относительный разброс ударов - к нулю. В результате энергия частицы E однозначно зависит от “объема” L, как будто объем с частицей становится похожим на сплошную упругую жидкость.

В адиабатическом пределе произведение длины отрезка L на скорость частицы v есть адиабатический инвариант:

Lv = const.

dE/2E = - dL/L, (1)

EL² = const. (2)

В таком случае изменение энергии частицы при движении вперед-назад обратимо, чем и вызывается необходимость холодильника.

Дальше. Давление есть отношение импульса, переданного частицей стенке, ко времени измерения. Нефлуктуирующему давлению классической термодинамики соответствует предел такого давления при больших временах измерения, что возможно в покое или в адиабатическом пределе:

P = 2E/L. (3)

Из (2) и (3) получается одномерный аналог адиабаты Пуассона:

PL³ = const.

Из (1) и (3) получается связь:

т.е. в адиабатическом пределе давление P оказывается обобщенной силой, сопряженной обобщенной координате L. Возникающее замкнутое термодинамическое описание как бы отображает особый мир, новую сущность, в которой частицы оказываются ненаблюдаемыми, отсутствуют.

Итак, для выигрыша в работе за цикл можно перед обратным ходом часть энергии частицы отдать “холодильнику”. Можно, но не обязательно.

VIII. НЕОБХОДИМОСТЬ ХОЛОДИЛЬНИКА
КАК СЛЕДСТВИЕ НЕТОЧНОГО КОНТРОЛЯ НАД СИСТЕМОЙ.

В принципе механика позволяет сжать объем без затраты работы. Адиабатические инварианты получаются при условии отсутствия параметрического резонанса. Можно, например, все время вдвигать поршень с любой скоростью, останавливая его лишь в моменты подлета к нему частицы, а после удара, не меняющего энергию, снова продолжать вдвигание. Или можно, скажем, выбрать момент, когда частица находится где-то в исходной области, и быстро задвинуть поршень (конец отрезка). Так можно поступать при любом числе частиц. Механике безразлично, сколько частиц имеется, у нее нет понятия “много”. Могут также сказать, что при большом числе частиц слишком долго ждать, когда же частицы соберутся в исходной части объема, чтобы задвинуть поршень. Но в механике нет понятия “долго”. Могут еще сказать, что при большом числе частиц слишком сложно вдвигать поршень, притормаживая его при подлетах каждой частицы. Но в механике нет понятия “сложно”. Все эти понятия есть не у механики, а у человека, который использует механику.

Если человек действует, не используя всех возможностей механики, то результат может быть хуже, чем тот наилучший, который в принципе достижим при использовании всех ее возможностей. В конечном счете важно не то, что вообще можно сделать, то есть что вообще позволяет сделать мир, а то, что делается реально. Для достижения некоторого результата важен реальный контроль, а почему реализуется именно этот контроль - это уже другой вопрос, ответы на который могут быть разнообразными. Пусть, например, мы научились хорошо управлять и можем сделать машину без холодильника. Но ведь хуже работающую машину мы всегда можем сделать. Не станем же мы объявлять ее плохое качество прямым и неизбежным следствием свойств мира! И старые машины будут работать по-старому, и их работа будет описываться обычной термодинамикой - так не будем же мы в такой ситуации считать ее законы законами природы самой по себе, не зависимыми от специфической деятельности субъекта!

Термодинамические свойства, парадоксальные с точки зрения механики, появляются не из-за механики. Механика не порождает термодинамики, и нельзя считать, что порождает, не получая взамен парадоксов. Поэтому термодинамику нельзя вывести из механики, что обычно только и пытаются сделать, получая неожиданно всякие неясности, трудности, противоречия и парадоксы. Например: возвратная теорема не допускает необратимости; эргодичность невозможна из-за теоремы Брауэра об инвариантности размерности; квазиэргодичность не дает правильных времен релаксаций; для подсчета термодинамической вероятности вы разбили объем вертикально, а я горизонтально и получил другой результат, - кто же прав?

Большинство не видит принципиальных трудностей. Так, у И.Неймана [6] читаем: “...знание 2k параметров (при k степенях свободы. - В.Г.) позволило бы описать... поведение причинно, но теория газов использует лишь два: давление и температуру, которые являются определенными, сложными функциями этих 2k параметров.” Нет, неправильно. Они не являются функциями этих 2k параметров в том смысле, что не порождаются ими как, например, электрическое поле зарядом. Аналогичный дефект существует и в доказательствах запрета детерминистских субквантовых, так называемых скрытых, параметров. А.И.Ахиезер и Р.В.Половин в известной статье 72-го года в “Успехах физических наук” [7] рассматривают и в явном виде записывают квантовые наблюдаемые как функции скрытых параметров, после чего, естественно, приходят к выводу, что в таком случае квантовая механика была бы невозможна, а так как она все-таки есть, то субквантовые переменные должны отсутствовать. Обращение к подобнoй функциональной связи есть следствие не преодоленного редукционистского подхода, когда объект пытаются сводить к его элементам, как картину к краскам.

Итак, необходимость холодильника не следует из самой механики, а следует из характера контроля над частицами, над процессом передачи энергии от них поршню.

IХ. НЕОБХОДИМОСТЬ УПРАВЛЕНИЯ ДЛЯ ПОЛУЧЕНИЯ ЖЕЛАЕМОГО РЕЗУЛЬТАТА. В КАКОМ МИРЕ СУЩЕСТВУЕТ КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ ?

Посмотрим на смысл происходящего с тепловой машиной. У частиц газа в объеме есть энергия. Требуется ее использовать для совершения работы. В принципе можно с помощью манипуляций поршнем, основанных на точных замерах состояния частиц и механических расчетах, забрать у частиц всю энергию. Механика это позволяет. Но если такие точные и тщательные действия не делаются, если движения поршня не согласовывают, не коррелируют специально с состоянием частиц, то желаемый результат не может быть гарантирован. А в реальности они и не делаются: поршень движется, так сказать, наобум. Так как же тогда ожидать, что мы можем обойтись без каких-либо неприятностей типа нестопроцентного КПД?

Вопрос о контроле над системой для достижения некоторого результата поднимался уже очень давно. Тут можно вспомнить Максвелла и Сциларда.

Известная история с “демоном” Максвелла, достаточно точно контролирующим частицы и поэтому позволяющим обходиться без холодильника, - показательный пример того, как с водой выплескивают ребенка. Обоснованно или необоснованно показывая неосуществимость подобного устройства, опускали тот факт, что как раз плохой контроль - независимо от вызвавшей его причины - и соответственно плохое управление процессами и есть то, что совместно с механикой приводит к обычной работе тепловой машины, к необходимости для нее холодильника. Качество контроля в явном виде и надо было включить в обоснование термодинамики. А почему контроль именно такой - это уже другой вопрос. Однако из-за объективистской традиции ни к чему помимо механики не обращались, почему и оказалось невозможным объяснить термодинамику. Поэтому же и доказательства невозможности демона были тавтологичны: он, мол, перестанет различать частицы потому, что покраснеет (нагреется). И это по сути термодинамическое объяснение приводилось для обоснования термодинамики!

Итак, в модельном мире с классической механикой холодильник не является необходимым. Но могут сказать, что в реальном мире в случае многих частиц невозможно точно осуществить нужные движения поршня или другие подобные процедуры. Очень может быть, - но это надо доказывать независимо, не опираясь на еще не доказанную невозможность, в частности - на термодинамику. Сомнительно, что это вообще можно сделать.

Обратим внимание на смысл одного термина в термодинамике, совершенно, по-видимому, чуждого науке физике. Это КПД - коэффициент полезного действия. Кому полезного? Чисто объективному миру совершенно все равно, куда перейдет энергия частиц газа, лишь бы она сохранялась. Объективного подразделения по критерию полезности нет. Это человек подразделяет части энергии на полезные и бесполезные. У него есть заинтересованность одновременно со слабостями, ему удобно или неудобно, сподручно или несподручно работать с тем или иным размещением энергии по объектам. А не направляемое специальным и достаточным образом движение энергии не всегда приводит к желательному для человека результату. Тут и возникает нестопроцентный КПД.

Нельзя некритично связывать результат только со свойствами природы, как это делалось при объяснении необходимости холодильника и нестопроцентного КПД. Пусть, скажем, мы вообще ничего не предпринимаем для получения работы. Не будем же мы в этом случае возводить неполучение работы в ранг закона природы!

X. КОНТРОЛЬ НАД ЧАСТИЦАМИ С ПОМОЩЬЮ МАКРОПАРАМЕТРОВ ХАРАКТЕРИЗУЕТСЯ НЕНУЛЕВОЙ НЕТОЧНОСТЬЮ В ДЕЙСТВИИ.

Попробуем теперь описать качество контроля. На адиабате по отношению к макропеременным он вполне однозначен. Но по отношению к микропеременным однозначности нет.

Ясно, что частицы контролируются с помощью стенок. Очевидно, этот контроль не очень хорош, непосредственная связь с объектом контроля внутри объема отсутствует, там координата в соответствующей степени неопределенна - по отношению к задаче управления. В принципе дело можно было бы поправить, если отмечать времена ударов о стенки, да и места ударов, а затем по механике пересчитывать последующее движение частиц. Но при работе машины ничего этого не делают, а за временем вообще не следят. Поршень движется не на основании точных механических данных и расчетов, а как бог ему на душу положит. И не важно, почему не делают и не следят. Не делают и всё - результат будет зависеть от того, что действительно делают.

Оценим неточность реального контроля над частицами, осуществляемого с помощью данных об объеме и давлении.

Предположим, что мы замеряем давление, которое в одномерном случае есть отношение импульса, переданного стенке, ко времени измерения. Предельное, бесконечно долго измеряемое давление реально не является наблюдаемым. Оно “наблюдаемо” лишь в идеальной схеме безвременной термодинамики. Итак, набираем удары за интервал D t (рис. 3). Пусть оказалось n ударов. Давайте проверим еще раз. Снова ждем в течение интервала D t, правда, положение интервала специально не выбираем - соответственно отсутствию специального выбора временного характера движения поршня. Тогда число ударов может оказаться отличным от первого на единицу.

Рис. 3.

Следовательно, давление мы будем знать с неточностью 2p/D t, где p - импульс частицы. Если теперь мы захотим найти энергию частицы, подставив данные об объеме и давлении в уравнение (3), то мы ее найдем, но с неточностью, обратно пропорциональной D t:

D = D E • D t ~ Lp.

Таким образом, контроль над микросистемой с помощью макропараметров характеризуется ненулевой неточностью в действии. Это приятно в двух отношениях.

1. Насколько я в курсе, до сих пор считается, что без квантовой механики никакой неопределенности в действии не бывает. Это понятно, так как на уровне самой механики это верно, а только об этом уровне физики почти всегда и думали. Важно то, что в нашем случае появился в чем-то похожий на квантовую механику пример замкнутой макромодели с детерминистскими скрытыми параметрами, но с неточностью в действии. При этом видно, что редукционистской связи между макро- и микроуровнями нет. Макроуровень - термодинамика - появляется только как отражение некоторых результатов определенного обращения с элементами микроуровня.

2. Во-вторых, появление неточности в фазовом пространстве желательно из-за того, что энтропию определяют как логарифм фазового объема, а с его появлением и поведением в классике есть очень большие проблемы.

XI. ЭНТРОПИЯ КАК ХАРАКТЕРИСТИКА НЕТОЧНОСТИ КОНТРОЛЯ. ТЕПЛОВАЯ ЭНЕРГИЯ - ЭТО ПЛОХО КОНТРОЛИРУЕМАЯ ЭНЕРГИЯ.

Ясно, что эта неточность в действии характеризует не систему саму по себе (частицы и стенки объема), а контроль над системой. Ясно также, что чем эта неточность больше, тем контроль хуже, грубее. А чем хуже контроль, тем меньше возможностей воспользоваться имеющейся кинетической энергией частиц, т.е. КПД ниже. Но аналогичным неприятным свойством обладает энтропия - ее рост связывают с нарастающим обесцениванием энергии.

Дальше. Известно, что энтропия сохраняется на адиабате. Но на ней же сохраняется и неточность контроля D - она есть адиабатический инвариант.

Тогда, во-первых, одинаковое поведение позволяет связать энтропию и неточность в действии функционально - просто одну величину заменять какой-то функцией от другой величины, скажем, S = S(D ). Во-вторых, из-за почти явной качественной близости этих двух величин в отношении возможностей использовать кинетическую энергию их надо бы связать и по существу. Причем очевидно, что неточность первична по отношению к энтропии, так как она объясняет причину и смысл обесценивания энергии. В-третьих, практически очевидно, что неточность следует подставить вместо фазового объема, логарифмом которого должна являться энтропия, а перед логарифмом должен стоять плюс. В таком случае записываем:

S = k ln(Lp) - S_o,

где S_o - начало отсчета. Понятно, что в классическом случае можно пользоваться только разностью значений энтропии в различных состояниях.

Между прочим, в термодинамике температура - величина не менее сложная, чем энтропия, и определяется она через энтропию: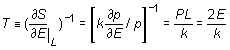

,

то есть на одну степень свободы (которая здесь у нас только и есть) приходится половина kT.

Таким образом, тепловая энергия - это не энергия “хаотического движения”, которое у классической механической системы не может быть определено, а в некотором смысле плохо контролируемая энергия. При точном механическом контроле у частиц есть кинетическая энергия, при рассмотренном же грубом контроле, когда и сами частицы не видны, она выступает уже как тепловая энергия.

Отмечу кратко, что аддитивность энтропии является не следствием тождественности частиц (тем более квантовой - как будто в классическом мире тепловая машина не работала бы обычным образом), а следствием динамики процессов, когда давление зависит только от суммарной энергии частиц.

XII. НЕОБРАТИМОСТЬ ОГРУБЛЕНИЙ ТЕРМОДИНАМИЧЕСКОГО КОНТРОЛЯ.

Вернемся к рассмотренному циклу тепловой машины. После расширения по адиабате ввиду обратимости движения по ней часть тепла надо сбросить в холодильник. Как это сделать?

Будем представлять холодильник также в виде объема с газом той же плотности, что и в цилиндре в конце расширения, но более низкой температуры. Приведем оба объема в тепловой контакт или просто уберем перегородку. Первоначальный контроль макропараметрами над двумя отдельными объемами теряется, возникает контроль над всем газом в суммарном объеме. В результате контроль очевидно ухудшается, а энтропия возрастает.

Обычно говорят, что газы из двух объемов при убирании перегородки перемешаются, произойдет их взаимная диффузия. Однако с точки зрения механики (математики), видящей только частицы, а не два газа как некие цельные, чем-то внутренним объединенные группы, перемешивание лишено смысла. Когда говорят, что частицы перемешиваются, когда одни из них появляются между другими, то выражаются неточно. Относительно самих по себе точек в объеме нельзя сказать: что одни точки находятся между другими. А вот с точки зрения контроля более грубого, чем механический, можно и естественно говорить о подразделении частиц на группы, по-разному контролируемые.
И только по отношению к такому неточному контролю,
в частности к контролю с помощью параметров объем и давление, можно говорить, что при убирании перегородки газы перемешаются, более подробный контроль сменится менее подробным. При таком “перемешивании” результирующая температура достигается однозначно:

,

где T₁, T₂, N₁, N₂ - исходные температуры и числа частиц в двух объемах. Всегда, без флуктуаций

max{T₁,T₂} і T і min{T₁,T₂},

S і S₁ + S₂.

После этого разделить газы по прежним объемам с возвращением первоначальных значений температур практически нельзя в рамках контроля с помощью макропараметров, не прибегая к точным механическим манипуляциям. Контроль с помощью макропараметров предлагает для обратного разделения объемов только один способ: введение перегородки наугад. Тогда, по Смолуховскому же, мы получим у разделенных объемов одинаковые температуры. А в термодинамической модели объем с однородной рабочей “жидкостью” делится перегородкой на части вполне однозначно. При таких действиях вернуться к исходному неравновесному состоянию практически невозможно.

Возражение против такой необратимости, основанное на возвратной теореме Пуанкаре, снимается пониманием, что макросостояние, и в частности его параметр - энтропия, не является функцией фазовой точки системы частиц. Поэтому возвращение фазовой точки в e -окрестность исходной точки не приводит автоматически к возвращению макросостояния. Макросостояние можно было бы вернуть в тот момент, но для этого надо было бы специально произвести действия, основанные на знании микросостояния. А такие действия в рамках грубого термодинамического контроля не определены.

Таким образом, огрубление термодинамического контроля в рамках этого контроля строго необратимо. Вот что в действительности необратимо: потеря контроля в рамках грубого контроля. Кратко говоря, термодинамическая необратимость - это не закон природы, а закон управления.

XIII. ЭНТРОПИЯ БЕЗ СУБЪЕКТА НЕ СУЩЕСТВУЕТ.

Сделаю общее методологическое заключение о смысле и месте энтропии. Помимо двух свойств наблюдателя, которые существенно использовал Смолуховский, здесь понадобились еще более субъективные вещи: это заинтересованность и наличие цели и действий той или иной точности. Сама энтропия как характеристика контроля не существует без субъекта. Это первый отчетливый пример физической величины, которая не существует без субъекта. Энтропия вообще не является характеристикой системы самой по себе - ни точной, ни приближенной. Она никак не указывает место системы в фазовом пространстве, а только указывает размер неопределенности, с которой контроль “видит” систему в этом пространстве. Полезное ее значение заключается в том, что она, будучи использована вместе с характеристиками реального состояния, может дать оценку качества результатов, получаемых при таком контроле. Но, конечно, в сфере замкнутой в себе феноменологической термодинамики, которая не видит ни частиц, ни времени, энтропия выступает как реальная функция состояния этого “термодинамического мира”.

Изложенные и связанные с ними вопросы рассмотрены в работах [8-16].

XIV. ДОПОЛНИТЕЛЬНЫЕ ЗАМЕЧАНИЯ

1. Когда система термодинамическая? Термодинамика, как считали и считают, имеет дело с системами (или наборами, конгломератами) с большим числом частиц. Но ответ таков: система механическая - если есть хороший контроль. В той мере, в какой он хорош, она выступает как механическая. Если же он плох (типа термодинамического), то система выглядит, представляется как термодинамическая.

Когда система механическая? Да когда ее хорошо контролируют. Например, отдельно лежащий большой и хорошо видный камень - явно представляется нам механическим. Даже если мы его не сдвинем с места, он для нас выглядит в принципе контролируемым. Вращающиеся части станка - тоже для нас механические, так как они приемлемых размеров, их число обозримо и с ними мы в состоянии достаточно точно оперировать. Электрическая энергия в проводах - тоже хорошая, поскольку хорошо контролируема.

2. Неверны иллюстрации термодинамической вероятности состояния как объективной характеристики наличного материала (безотносительной к контролю) с помощью картинок с мысленным разбиением объема на части с последующим подсчетом полиномиальной вероятности. Это ясно уже по тому, что различные разбиения, приводящие к разным ответам для одного и того же расположения одних и тех же частиц, объективно равновозможны, ни одно из них не предпочтительнее другого. Никакого объективно выделенного разбиения нет.

Однако указанная иллюстрация не вовсе ошибочна и бессмысленна. Только она изображает условную оценку состояния - как если бы объем был действительно разбит данным образом перегородкой и с так разбитой системой проводились манипуляции с помощью термодинамического контроля. То есть картинка иллюстрирует оценку системы по отношению к контролю при таком-то разбиении, если бы оно было осуществлено реально. О том, что эта оценка относится именно к реальным действиям, а не к системе самой по себе, говорит тот факт, что на картинках показывают простые формы разбиения - прямыми линиями и к тому же проведенными по простому: вертикально или горизонтально. Здесь явно видно влияние, отпечаток типичного характера человеческой деятельности: в ней простые действия предпочтительнее, а слишком сложные невозможны. А если бы кто стал играть в объективность и выбирать разбиения случайным образом из мешка, в котором собраны все абстрактно возможные разбиения, то вероятность выбора показываемых на картинках простых разбиений оказалась бы равной нулю. Аналогичное можно сказать о числе и размерах подобъемов, на которые следует разбивать исходный объем. Ведь и действительно иногда возникал вопрос: на сколько объемов надо разбивать объем, когда следует остановиться или надо разбивать до бесконечности? Так вот надо разбивать объем на столько подобъемов, на сколько это собираются сделать в реальности, а до бесконечности мельчить вообще не следует, так как на практике это не может быть осуществлено, а безотносительно к практике подобные оценки лишены смысла.

3. Часто интуитивно, как бы естественным образом, оценивают степень равновесности и отклонение энтропии от максимума у распределений газовых масс, даже не замкнутых: там-то плотное облако горячих газов, в другом месте - тоже много газа, но более холодного, и т.д. Следовательно, эта система еще далека от равновесия, она будет стремиться к большему равновесию, и ее энтропия будет возрастать. В такой оценке содержится следующее рациональное зерно.

Дело в том, что неявно фактически об этих облаках газов думают не в механическом смысле, когда можно сколь угодно точно контролировать все частицы по отдельности, а именно в термодинамическом смысле, который реально существует только в связи с таким грубым контролем. Так вот если бы указанные области газов были бы по отдельности окружены стенками и с полученными объемами с газом производилась бы работа обычным в термодинамике образом, то для каждого объема получилась бы энтропия как характеристика термодинамического контроля, а энтропия всей системы была бы равна сумме энтропий этих объемов. Безотносительно же к контролю никакого понятия равновесности и энтропии не существует. Дальше. При том, что в действительности объемов, окружающих газовые облака, нет, эти облака будут разбегаться и перемешиваться, так что вся система будет переходить к большему равновесию с возрастанием энтропии. Но это последнее изменение также имеет смысл только по отношению к новому выделению областей газа стенками по приблизительно устанавливаемым границам неоднородностей, как и оценка исходного состояния.

[ Предыдущая статья книги] [ Следующая статья ] [ На оглавление книги ] [ На главную страницу сайта]